Wprowadzanie sił wewnętrznych w IDEA StatiCa Detail

IDEA StatiCa Detail jest zaawansowanym narzędziem inżynierskim służącym do analizy obszarów konstrukcji zwanych strefami nieciągłości. W tych strefach trajektorie naprężęń ściskających i rozciągających odginają się, a przewidzenie ich przepływów stanowi wyzwanie dla projektanta.

Przeznaczenie programu implikuje konieczność „wycinania” poszczególnych elementów z konstrukcji, co z kolei może nastręczyć nam trudności. Jednym z wyzwań jest przeniesienie sił wewnętrznych z modelu prętowego na model ES typu tarczowego zastosowany w programie. Developerzy IDEA StatiCa znaleźli rozwiązanie dla tego problemu. W pobliżu uciętego końca elementu powstaje specjalna „Strefa transferu de Saint Venanta” – fragment modelu o bardzo dużej sztywności, w którym dzięki wiązaniom wielopunktowym siły przekrojowe są przenoszone na węzły siatki ES. Z doświadczenia wiem jednak, że sposób wprowadzania sił wewnętrznych w programie sprawia trudność wielu osobom, ponieważ stosuje podejście nieco odmienne od typowych programów do statyki. W poniższym artykule postaram się w sposób wyczerpujący wytłumaczyć jak podejść do tego zagadnienia na kilku typowych przypadkach.

Belki

Zacznijmy od rzeczy najprostszych. Programem ze stajni IDEA StatiCa dedykowanym belkom żelbetowym i sprężonym jest oczywiście IDEA StatiCa Beam (jak sama nazwa wskazuje). Jednak jeżeli chcemy policzyć belkę z otworami lub podciętą w strefie przypodporowej potrzebny nam będzie Detail.

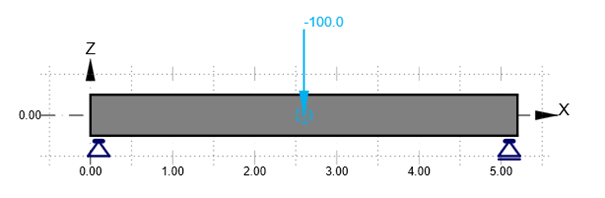
Przeanalizujmy żelbetową belkę jednoprzęsłową, swobodnie podpartą o rozpiętości 5 m, obciążoną w środku rozpiętości siłą skupioną o wartości 100 kN. Przekrój 500x300mm, beton C30/37.

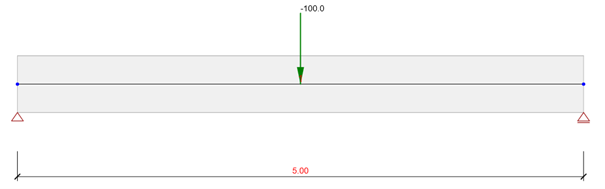
Jako inżynierowie nie musimy się zanadto zastanawiać nad wartościami reakcji i sił w tym przypadku – wystarczyłby nam kawałek kartki by naszkicować wykresy. Ja jednak (aby rozwiać wszelkie wątpliwości) użyłem Aplikacji Beam.

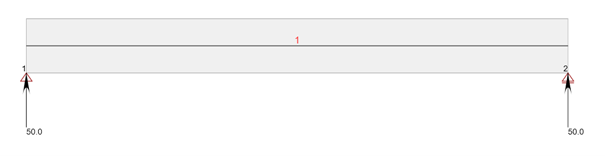
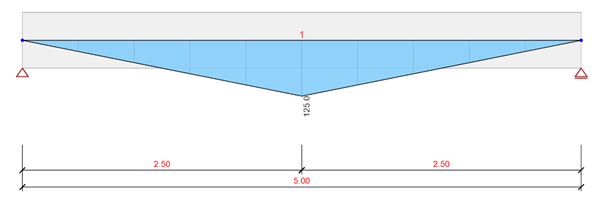
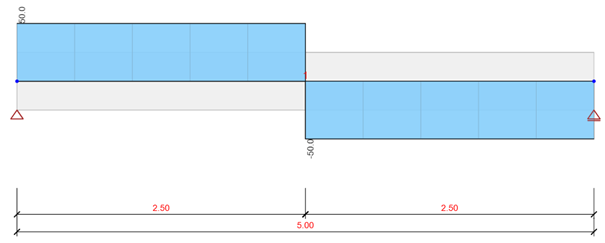
Teraz przejdźmy do Detail i myślowo (oraz w Detailu 😉 ) wytnijmy sobie strefę przypodporową naszej belki.

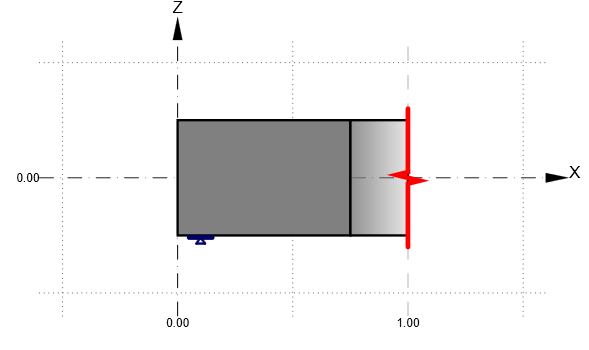
Tworzymy prosty model, długość 1 m, podpora i wycięty koniec. Tutaj pojawia się pierwszy „smaczek” pracy z Detail – podpora zawsze ma jakąś szerokość a nie jest punktowa jak w modelu wyidealizowanym. Niemożliwe jest więc podparcie belki na samej krawędzi – zawsze jest odrobinę od niej odsunięta, co ma spore znaczenie w momencie przykładania sił, ale do tego wrócimy.

Tworzę pierwszy przypadek obciążenia i tutaj zaczyna się nasz dzisiejszy temat.

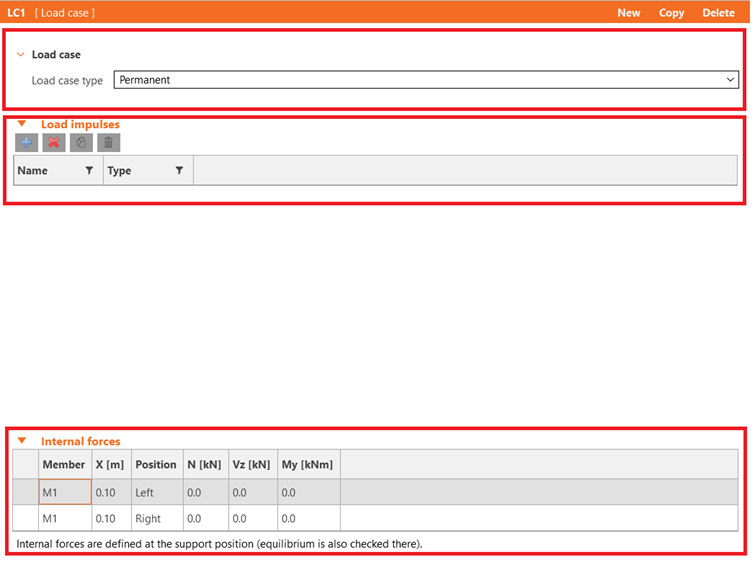
Ustawić możemy naturę przypadku (stałe, zmienne lub sprężenie, ale ten ostatni dostępny jest jedynie w przypadku pełnych belek). Mamy również dostęp do wprowadzania impulsów obciążenia (czyli po prostu wprowadzania obciążeń) oraz kluczowej dla nas tabeli sił wewnętrznych.

W naszym przypadku tabela jest bardzo prosta, ale i tak wymaga pewnego wytłumaczenia.

W przypadku gdy mamy tylko jedną podporę, do dyspozycji mamy dwa wiersze odpowiadające lewej i prawej stronie podpory. Oznacza to że różnica między wartościami sił wprowadzonych do tabeli będzie reakcją podporową, na podstawie której program wyznaczy dalszy przepływ naprężeń. W przypadku belki swobodnie podpartej interesuje nas tak naprawdę wyłącznie wartość siły tnącej (brak momentów w podporze przegubowej; brak siły normalnej), wprowadźmy więc znaną nam już wartość reakcji na lewej podporze.

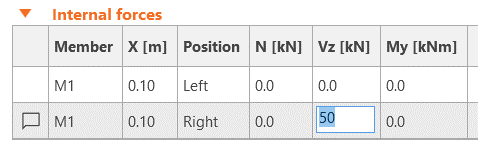
Jak widać program poprawnie przewiduje rozkład sił w dalszej części elementu. Wartość momentu 45 kNm (zamiast 50kNm wynikających z długości belki 1 m) wynika z konieczności odsunięcia podpory od krawędzi.

Skoro to już wiemy, pójdźmy o krok dalej i przedłużmy naszą belkę do docelowej długości 5 m (u nas 5,1 m) oraz obciążmy ją siłą skupioną w odległości 2,5 m od podpory.

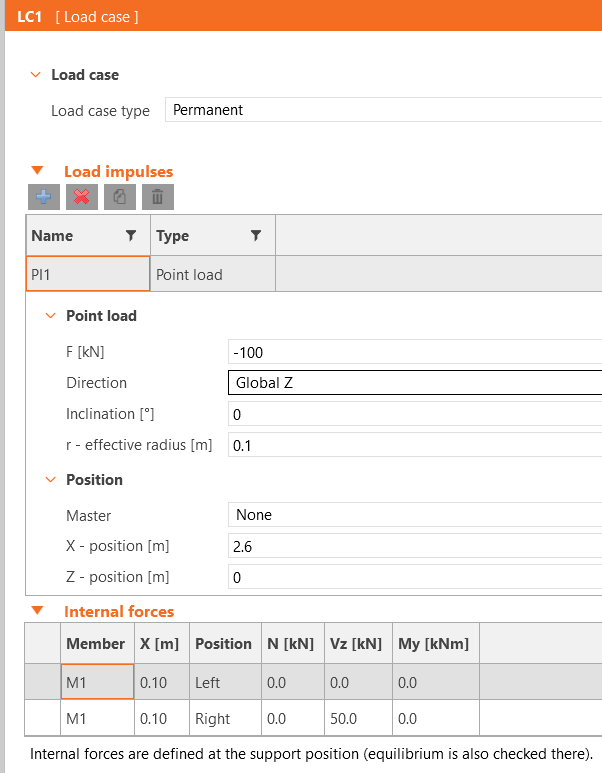
Jak widać osiągnęliśmy dokładnie taki rezultat jakiego się spodziewaliśmy. Na końcu belki wartość momentu wyniosła zero, zaś wartość siły tnącej po skoku o 100 kN w środku rozpiętości pozostała na tym samym poziomie.

Chce w tym miejscu zaznaczyć, że nie jest to przykład „sensowny” – badanie belki przyciętej traci sens jeśli ucinamy więcej niż jej połowę. W tym przypadku powinniśmy już zbudować pełny schemat statyczny co pozwoliłoby nam na np. lepsze sprawdzenie ugięcia.

W momencie gdy mamy pełny schemat statyczny (statycznie wyznaczalny lub niewyznaczalny to bez różnicy) program już nie rysuje nam wykresów sił, nie mamy też możliwości ich tabelarycznego przykładania. Model obciążamy wówczas wyłącznie przy pomocy impulsów obciążenia. Wynika to z natury modeli w Detail, zbudowanych z elementów tarczowych. Program, dopiero przy obliczeniach, przelicza naprężenia w betonie. Aby wyznaczyć siły wewnętrzne należałoby zatem scałkować wartości naprężeń po wysokości przekroju. Taka funkcja nie została jednak zaimplementowana w programie.

Myślę że przypadek wprowadzania sił wewnętrznych w belkach został omówiony w sposób wyczerpujący. Przejdziemy teraz do rzeczy nieco trudniejszych (choć może tylko z pozoru).

Węzeł narożny

Kolejnym przykładem, który chce omówić jest węzeł narożny, którym szczegółowo zajmowałem się w serii IDEA StatiCa Concrete od A to Z.

Link do filmu.

Wybrałem go ponieważ jest on elementem pośrednim między belką a węzłem wewnętrznym/wspornikiem gdzie do węzła dochodzą 4 elementy.

Stwórzmy przykładowy model i przeanalizujmy przypadek LC1.

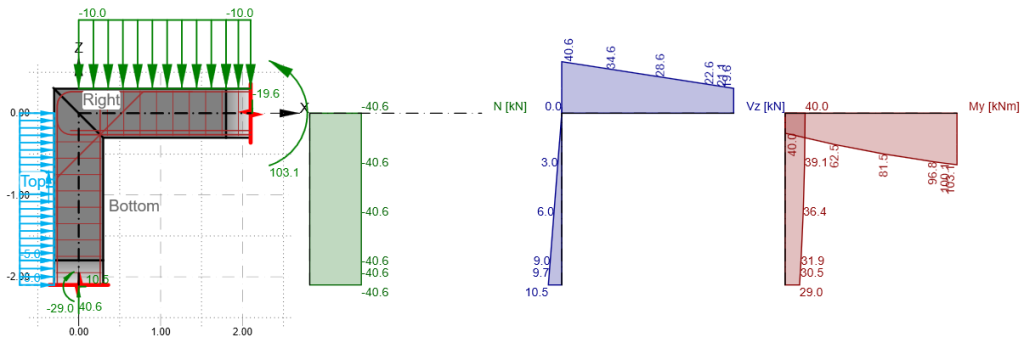
Tym razem nie będziemy nic zmieniać w modelu. Omówimy sobie tylko wprowadzone już siły i obciążenia.

Spójrzmy na słup. Mamy w nim wprowadzoną wartość siły normalnej -40,6 kN. Pozostaje ona stała na długości słupa, ponieważ nie ma żadnego obciążenia, które mogłoby ją zredukować.

Wprowadzony mamy również moment zginający o wartości 40,0 kNm. Tak samo jak w przypadku siły normalnej wartość, którą wprowadzamy przyłożona jest do węzła słup-belka. Następnie moment jest redukowany na długości słupa przez przyłożone obciążenie ciągłe. Odbywa się to na zasadzie prostej sumy momentów względem końca belki. Przeliczmy to:

\(\Sigma_{M_{S-2,1}} \left( 40 – 5 \times 2.1 \times \frac{2.1}{2} \right) = 28.975 \approx 29 \, \text{kNm}\)

Tak samo sprawa ma się z siłami w belce. Wprowadzona wartość momentu w węźle 40,0 kN, zaś siła normalna ze słupa naturalnie przeszła nam w siłę tnącą o wartości 40,6 kN. Siłę w słupie traktujemy jako reakcję podporową, a następnie uwzględniamy przyłożone obciążenie ciągłe o wartości -10kN/m.

Znowu możemy policzyć sumę momentów względem przyciętego końca elementu.

\(\Sigma_{M_{B_{2,1}}} \left( 40 + 40.6 \times 2.1 – 10 \times 2.1 \times \frac{2.1}{2} \right) = 103.21 \approx 103.1 \, \text{kNm}\)

(Delikatna rozbieżność wynika z zaokrągleń. Rzeczywista wartość wprowadzonej siły to 40,55kN)

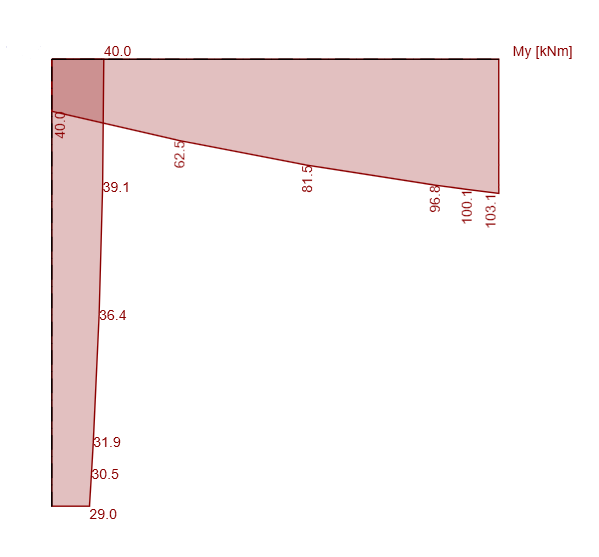
Jak widać obliczone przez nas sumy odpowiadają wynikom momentów z programu. Tak samo sprawa ma się z siłami tnącymi.

Podwójny wspornik

Przejdziemy teraz do ostatniego przykładu, sprawiającego najwięcej problemów – wspornika podwójnego. W tym celu znowu tworzę przykładowy projekt.

Tym razem utrudnimy sobie zadanie i zmodyfikujemy geometrię na sprawiającą więcej problemów.

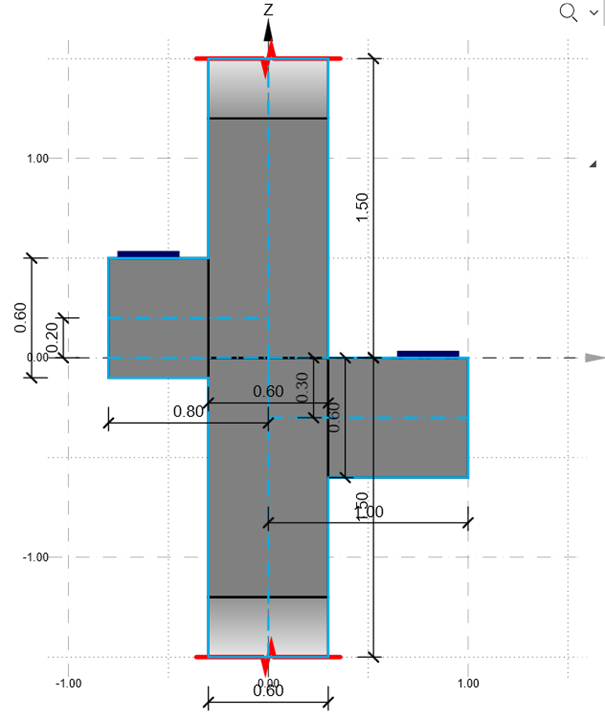
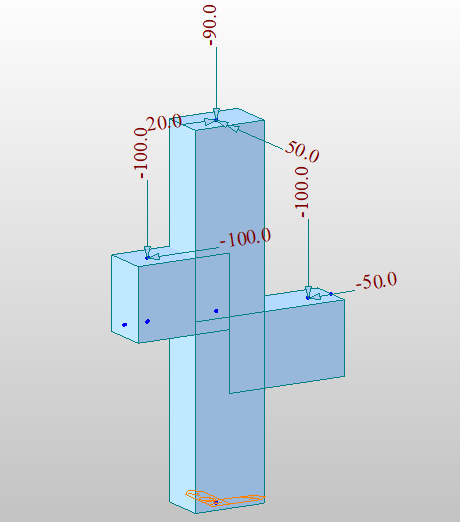
Następnie obciążymy nasze dwa niesymetryczne wsporniki siłami jak na rysunku.

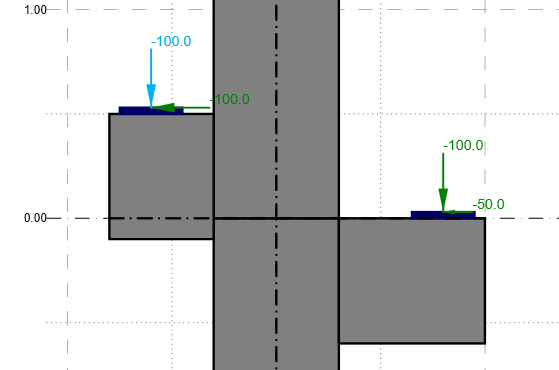
Zastanówmy się jak będą wyglądały wykresy sił wewnętrznych dla takiego układu.

Do prawego wspornika przyłożoną mamy siłę pionową -100 kN oraz poziomą -50 kN. Miejsce przyłożenia siły (choć na rysunku tego nie widać, ale wiemy to na podstawie lokalizacji płyty łożyskowej) znajduje się 80 cm od osi słupa a jego górna krawędź leży na osi poziomej modelu. Główne osie modelu zawsze pozostają w tym samym miejscu, niezależnie od pionowego offsetu wsporników, siły wewnętrzne rozważamy względem tego układu. Łatwo więc policzyć, że dla prawego wspornika równania równowagi (dla punktu 0,0 głównego układu) będą wyglądały następująco:

\(\Sigma_{M_P} \left( -100 \times 0.8 – 50 \times 0 \right) = -80 \, \text{kNm}\)

\(\Sigma_{V_P} \left( 100 \right) = 100 \, \text{kN}\)

\(\Sigma_{N_P} \left( -50 \right) = -50 \, \text{kN}\)

Do lewego wspornika również przyłożoną mamy siłę pionową -100 kN a także siłę poziomą -100 kN. Kluczowe w tym przypadku jest dla nas ustawienie wspornika względem głównych osi układu – jest on przesunięty w górę o 20 cm. Górna krawędź znajduje się więc 50 cm (wysokość przekroju h = 60 cm; połowa wysokości + offset = 50 cm) nad główną osią poziomą, zaś siła pionowa przyłożona jest 60 cm od środka układu. Ułóżmy równania równowagi dla lewego wspornika:

\(\Sigma_{M_L} \left( -100 \times 0.6 – 100 \times 0.5 \right) = -110 \, \text{kNm}\)

\(\Sigma_{V_L} \left( -100 \right) = -100 \, \text{kN}\)

\(\Sigma_{N_L} \left( 100 \right) = 100 \, \text{kN}\)

Teraz rozważmy górną część słupa. Przyłożone we wspornikach siły nie mają wpływu na siły wewnętrzne powyżej i odwrotnie – siły w słupie nie zmienią nam układu sił we wspornikach. Aby rozważyć sytuacje, w której słup jest już w jakiś sposób obciążony w swojej górnej części załóżmy sobie pewne siły wewnętrzne w nim:

\(M_y = -80 \, \text{kNm}\)

\(V_z = 20 \, \text{kN}\)

\(N = -90 \, \text{kN}\)

Skoro wiemy już wszystko o siłach w pozostałych elementach przejdźmy do podstawy czyli dolnej części słupa. W tym celu musimy obliczyć superpozycje sił wewnętrznych z pozostałych 3 elementów dla środka głównego układu współrzędnych modelu.

\(\Sigma_{M_{(0;0)}} \left( 110 – 80 – 80 \right) = -50 \, \text{kNm}\)

\(\Sigma_{V_{(0;0)}} \left( -100 – 50 + 20 \right) = -130 \, \text{kN}\)

\(\Sigma_{N_{(0;0)}} \left( -100 – 100 – 90 \right) = -290 \, \text{kN}\)

Wiedząc to wszystko nie zwlekajmy i wprowadźmy obliczone siły do programu zamieniając niezrozumiałe po przyłożeniu samych sił wykresy na coś sensownego.

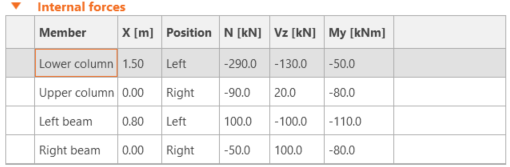
Nasze wykresy obecnie wyglądają w następujący sposób:

Otrzymane wykresy wyglądają prawidłowo. Zastanawiać mogą nas jedynie zmiany wartości momentów wzdłuż słupa. Przyłożyliśmy przecież wartości -80 kNm i -50 kNm. Skąd inne wartości na końcach? Są one oczywiście logiczne, ponieważ nasze siły w tabeli przykładamy dla środka głównego układu osi. Od tego miejsca siły tnące w słupie traktowane są jak przyłożone w tym miejscu siły skupione, stąd dla końców słupa:

\(\Sigma_{M_{(0;1.5)}} \left( -80 + 20 \times 1.5 \right) = -50 \, \text{kNm}\)

\(\Sigma_{M_{(0;-1.5)}} \left( -50 + 130 \times 1.5 \right) = 145 \, \text{kNm}\)

Teraz wszystko się zgadza, jednak dla pewności postanowiłem przeprowadzić weryfikację. W tym celu stworzyłem identyczny model wspornika w programie MIDAS Civil. Aby uwzględnić taką pracę elementu jak w Detail – górną krawędź słupa pozostawiłem wolną, zaś w podstawie zastosowałem utwierdzenie. Spójrzmy co z tego wyszło:

Specjalne podziękowania w tym miejscu należą się Pani Dominice Grzegorczyk, która pomogła mi rozwiązać problem z przyłożeniem sił w lewym wsporniku – „rigid link” załatwił sprawę 😉

Po przeprowadzeniu analizy wyniki wyglądają następująco:

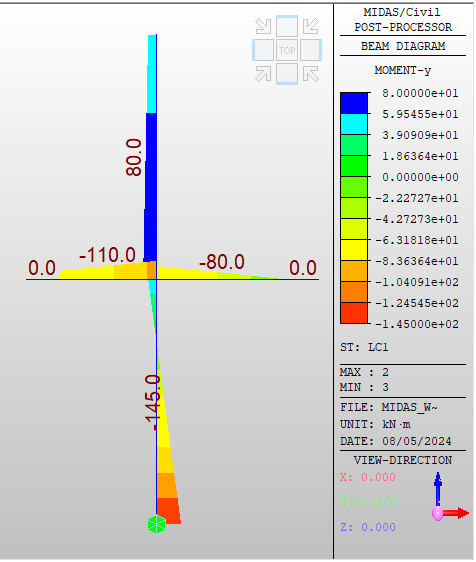
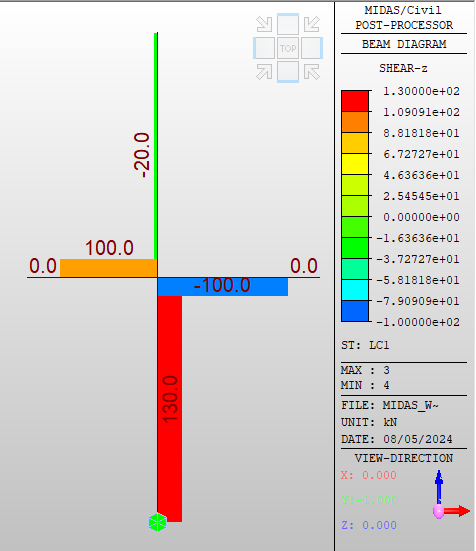
Jak widać na powyższych zrzutach ekranu, wykresy sił wewnętrznych w Midasie wyszły nam takie same jak w Detail. Jedyna rozbieżność zachodzi w konwencji znakowania sił tnących, jednak nie ma to dla nas dużego znaczenia (wynika to z przyjętego układu a tym samym konwencji formułowania równań równowagi).

Podsumowując nasze dzisiejsze rozważania. Wprowadzanie sił wewnętrznych w Detail wymaga pewnego wysiłku. Jest ono jednak logiczne i łatwe do przyswojenia, jako że zazwyczaj wprowadzamy element, którego statykę znamy z modelu globalnego. Jak każdy program od IDEA StatiCa, ze względu na swoje zaawansowanie i specjalistyczny charakter, Detail wymaga by do niego przysiąść i przyswoić pewne zawiłości. Po opanowaniu obsługi oraz zrozumieniu mechanizmów działania programu stanowi on narzędzie znacznie ułatwiające pracę projektanta konstrukcji.

Autor: Julian Haudek

Kontakt: j.haudek@jde.com.pl