Algorytm projektowania elementów sprężonych w Detail
W tym artykule dowiesz się jak zamodelować elementy strunobetonowe, jak przyłożyć obciążenia oraz określić straty sprężania i zasymulować straty sprężenia w aplikacji Detail. Wykonamy analizę liniową prostej belki w aplikacji Beam oraz porównamy wyniki z uzyskanymi w Detail.
Wprowadzenie i założenia
Zacznijmy od krótkiego opisu oprogramowania IDEA StatiCa do projektowania konstrukcji betonowych. Artykuł ten w głównej mierze dotyczy projektowania konstrukcji sprężonych w aplikacji Detail, która służy głównie do obliczania stref nieciągłości lub całych elementów zawierających stref nieciągłe takie jak otwory, podcięte końce itp.
Dla porównania wyników użyjemy aplikacji Beam której celem (jak nazwa wskazuje) jest projektowanie belek żelbetowych.
Musimy w tym miejscu przedstawić kilka założeń i ograniczeń by dobrze rozumieć sposób obliczenia elementów sprężonych w Detail.
- Analiza zależna od czasu (etapowanie) nie jest wprost zaimplementowane w Detail. Mamy ją do dyspozycji w Beam gdzie prowadzanie kolejnych etapów jest szybkie i proste.
- Etapowanie może zostać w Detail zasymulowane poprzez umiejętne zarządzanie inkrementacjami w poszczególnych kombinacjach oraz edycję współczynników pełzania.
- Detail nie uwzględnia skurczu oraz obciążeń termicznych
- Przenoszenie przez beton rozciągania jest w Detail całkowicie wykluczone. Dlatego dla naszego porównania wyników potrzebujemy belki niezarysowanej. Oczywiście takie same podejście można stosować do belek w których dopuszczamy zarysowanie jednak wyniki nie będą takie same w aplikacji Beam gdzie uwzględniona jest jedynie analiza liniowa
Inkrementacje
Przed przejściem do naszych przykładów musimy zrozumieć jak działają inkrementacje w kombinacjach zastosowanych przy projektowaniu elementów sprężonych w Detail.
W programie mamy do dyspozycji trzy natury przypadków obciążeń:
- Sprężenie – dla inkrementacji P
- Obciążenie stałe – dla inkrementacji G
- Obciążenie zmienne – dla inkrementacji V
Jeżeli utworzymy kombinację zawierającą przypadki obciążeń każdej natury, całość obciążenia od sprężenia zostanie przyłożona w pierwszej inkrementacji P, całość obciążenia stałego zostanie przyłożona w inkrementacji drugiej G, natomiast całość obciążenie zmiennego przyłożona zostanie jako ostatnia inkrementacja V.
Jest to spowodowane faktem że program, obliczając kombinacje SGU używa innych współczynników materiałowych dla poszczególnych inkrementacji (natur obciążenia). Dla kombinacji SGN używany jest tylko jeden model materiałowy zgodny z wybraną normą.
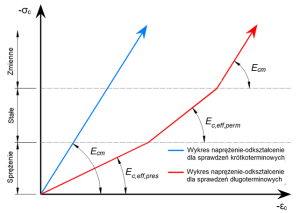
Jak widać na wykresie mamy 3 moduły sprężystości:
- \(E_{c,eff,press} = E_{cm} / (1+ \phi_{press})\) – Efektywny moduł sprężystości betonu dla inkrementacji P
- \(E_{c,eff,perm} = E_{cm} / (1+ \phi_{perm})\) – Efektywny moduł sprężystości betonu dla inkrementacji G
- \(E_{cm}\) – Sieczny moduł sprężystości betonu
Gdzie \(\phi_{press}\) i \(\phi_{perm}\) to współczynniki pełzania dla inkrementacji P i G. Współczynniki możemy zmienić w zakładce Materiały i Modele.
Zauważmy że dla efektów krótkoterminowych używany jest moduł \(E_{cm}\). Jest on odpowiedni dla wszystkich inkrementacji. Długoterminowe straty są brane pod uwagę tylko dla weryfikacji efektów długoterminowych.
Parametry belki
Dwa identyczne projekty zostały stworzone w aplikacjach Detail i Beam. Załączone zostały na końcu tego artykułu. Pobierz je i analizuj podczas dalszego czytania.
Przykład w Beam zostanie porównany z Detail na 3 etapach konstrukcyjnych.
Model stanowi strunobetonowa belka swobodnie podparta o przekroju dwuteowym z betonu klasy C45/50.
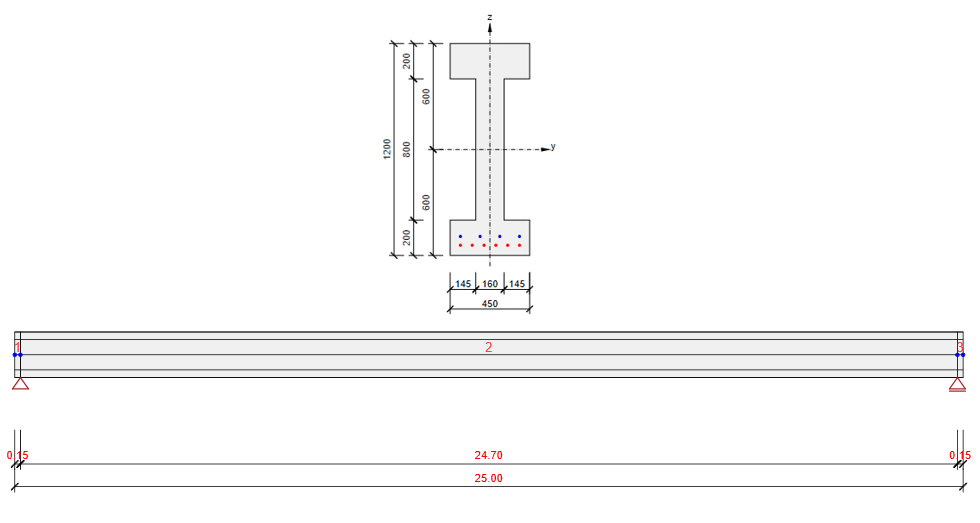
Będziemy wykonywać sprawdzenie w trzech etapach konstrukcyjnych:
- Pierwsze przeniesienie siły sprężającej – 2 dni (zaraz po zwolnieniu)
- Przyłożenie obciążeń – 60 dni (początek projektowanego czasu życia)
- Koniec projektowanego czasu życia – 18250 dni (50 lat)
Inne etapy mogą zostać wprowadzone w podobny sposób.

Jak można zauważyć użyliśmy definiowanego przez użytkownika modułu sprężystości betonu. Wynika to z faktu, że chcemy pokazać jak zachowuje się nasza belka która zaczyna przenosić siły wynikające ze sprężenia przed uzyskaniem przez beton normowej 28 dniowej wytrzymałości.
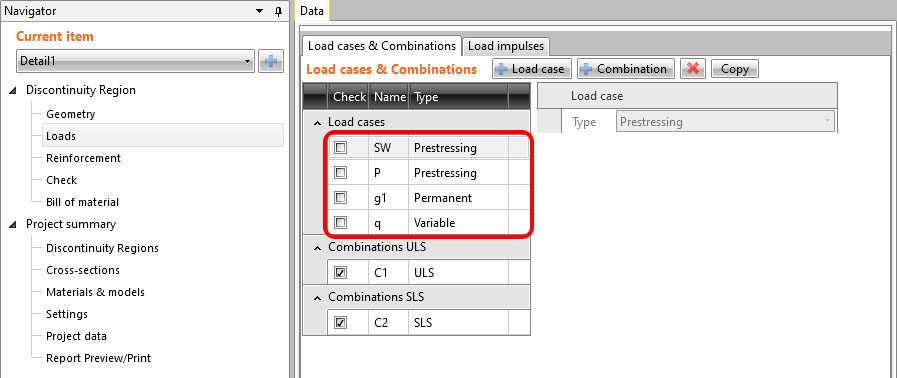
Przyłożone zostały jedynie 4 przypadki obciążeń. Numery w nawiasach są numerami etapów w których dane obciążenia są przykładane.
- Ciężar własny – SW (1)
- Sprężenie – PRE (2)
- Obciążenie stałe – G (6)
- Obciążenie zmienne – Q
Pozostałe przypadki obciążeniowe są puste.
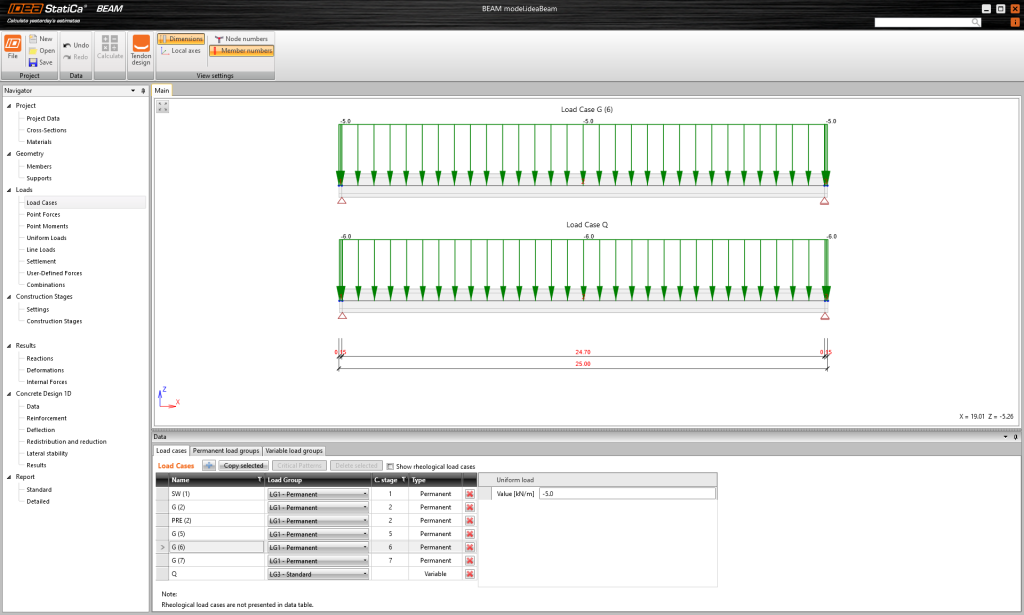
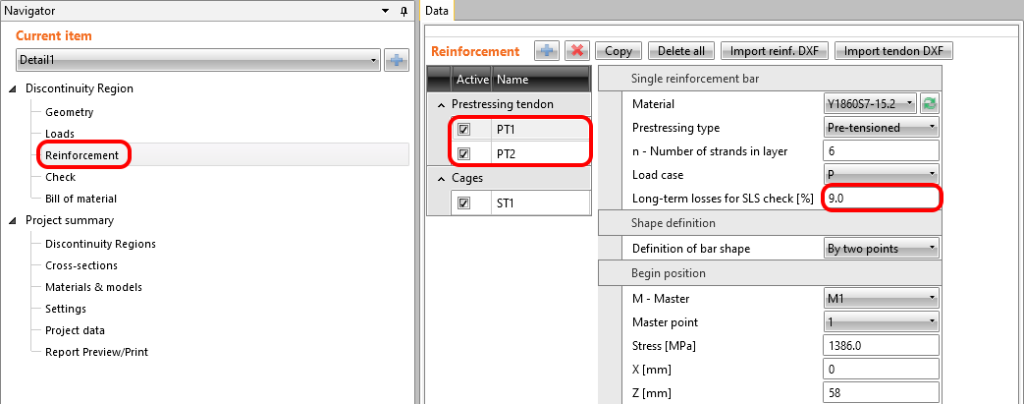
Teraz spójrzmy na sprężenie. Wprowadzono 2 rzędy splotów. Warto wspomnieć że niższy rząd został wyłączony na długości 3 m.
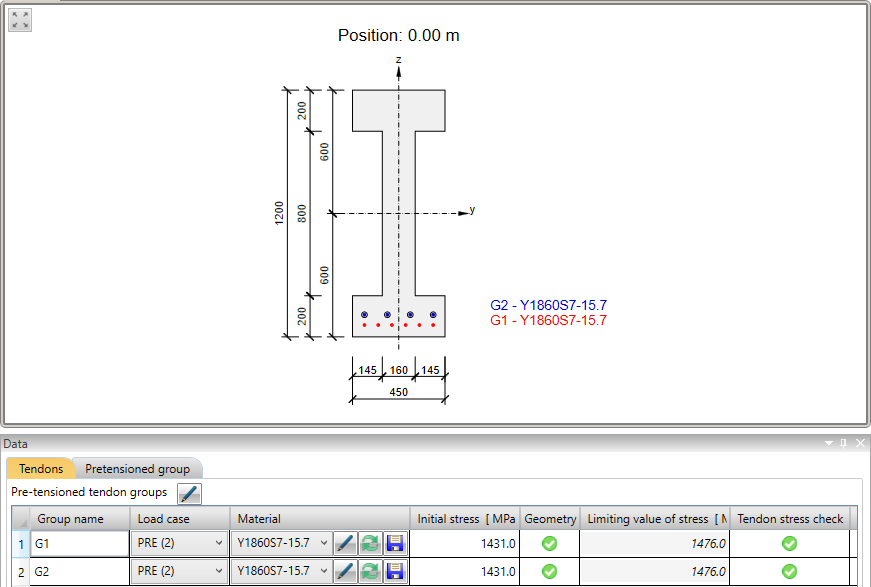
Jest kilka wartości naprężenia w cięgnach które powinniśmy kontrolować podczas przykładania sprężenia. W tym momencie pokrótce wyjaśnimy proces sprężenia oraz poszczególne wartości naprężeń oraz strat.
Proces sprężenia belki strunobetonowej
Etap 0 – naprężenie splotów → Sploty są ustawiane we właściwych pozycjach, kotwione po jednej stronie i naprężane od drugiej strony za pomocą siłownika.
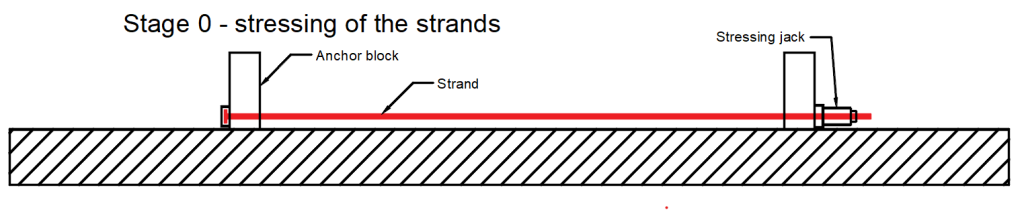
\(\sigma_{ pr,cor }\) – Naprężenie początkowe – maksymalne naprężenie podczas rozciągania pręta. Musi być mniejsze od – zgodnie z EN 1992-1-1 5.10.2.1. Jest to naprężenie na siłowniku. W naszym przykładzie .
Etap 1 – betonowanie → Układanie mieszanki betonowej wokół cięgien.
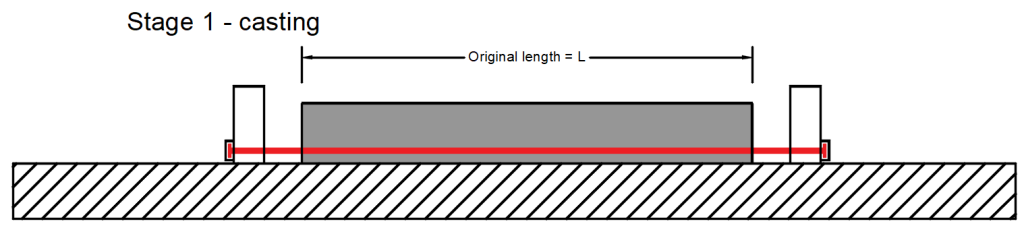
\(\sigma_{ pr,cor }\) – Naprężenie po krótkoterminowej relaksacji zawierające również wpływ poślizgu na kotwie oraz ewentualnego odkształcenia przyczółków. W naszym przykładzie \(\sigma_{ pr,cor } = 1415 MPa\).
Etap 2 – odcięcie cięgien → Sploty zostają uwolnione a w betonie zachodzi odkształcenie sprężyste.
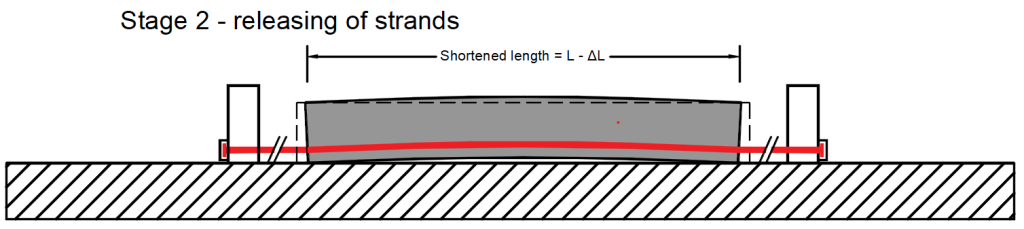
\(\Delta\sigma_{ PT }\) – Straty związane z różnicą temperatur między stalą sprężającą a formą.
\(\sigma_{pm0 }\) – Naprężenie zaraz przed uwolnieniem – Ta wartość jest wprowadzana w Detail. Jest to także wartość naprężenia przed stratami związanymi ze sprężystym odkształceniem betonu – \(\Delta{\sigma_{pe} } \) Jest ona obliczana jako \(\sigma_{pm0} = \sigma_{pr,cor} – \Delta \sigma_{pT}\) . W naszym przykładzie \(\sigma_{pm0} =1386 MPa\).
\(\Delta\sigma_{ pe }\) – Straty związane z odkształceniem sprężystym betonu.
\(\sigma_{pa}\) – Naprężenie po stratach krótkoterminowych. Innymi słowy jest to naprężenie po przeniesieniu siły sprężającej przez element. Jest ono obliczane jako \(\sigma_{ pa } = \sigma_{ pr,cor } – \Delta\sigma_{ pT } – \Delta\sigma_{ pe } =\sigma_{ pm0 } – \Delta\sigma_{ pe }\). W naszym przykładzie \(\sigma_{ pa } = 1319.2 MPa\).
Etap 3 – koniec projektowanego czasu życia
\(\sigma_{\infty } \) – Naprężenie po stratach długoterminowych
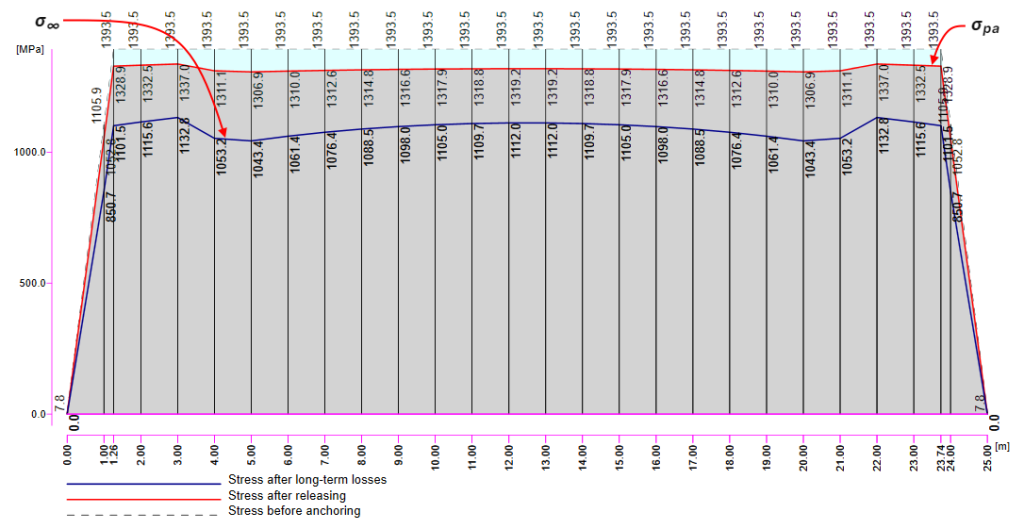
Teraz przypomnijmy sobie wykres naprężeń i strat gdzie ukazane zostały wartości \(\sigma_{ pa }\)(czerwona linia) oraz \(\sigma_{\infty } \) (niebieska linia).
Przeniesienie siły sprężającej
Model został zdefiniowany, przełączmy się więc do aplikacji Detail i zobaczmy jak zamodelować etap pierwszy. Geometria modelu pozostaje niezmieniona, dodaliśmy tylko strzemiona by przenieść ścinanie, nie wpłynie to jednak na interesujące nas wyniki.
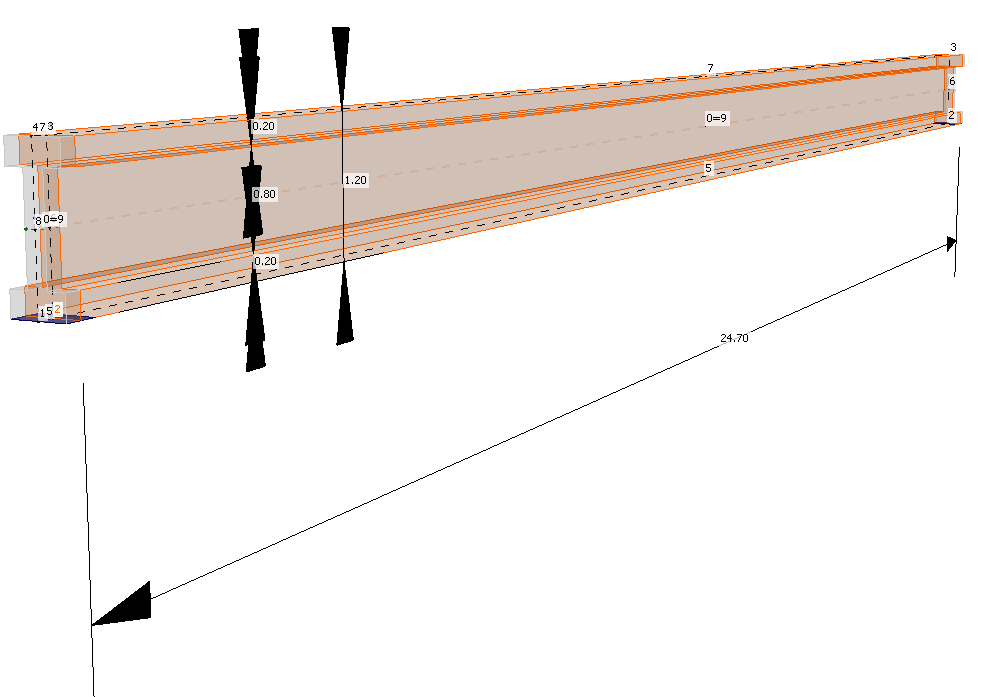
Dla tego etapu mamy tylko dwa przypadki obciążeniowe:
- SW – o naturze sprężenie (ciężar własny)
- P – również o naturze sprężenie (siła sprężająca)
Oba zostają przyłożone podczas pierwszej inkrementacji. Jak widać na poniższej ilustracji długo terminowe straty dla kombinacji SGU ustawione na 0%.
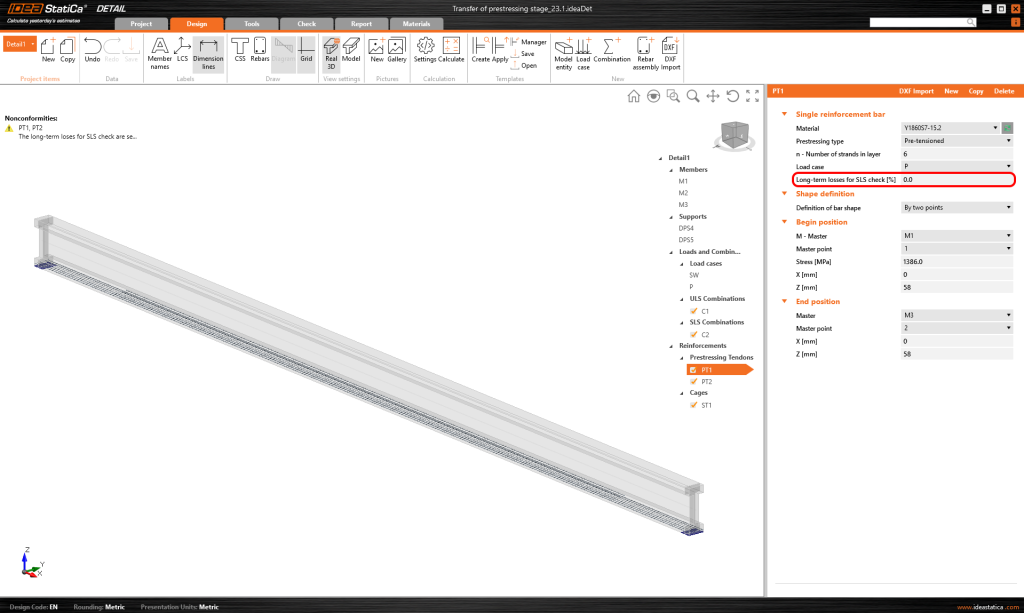
Współczynniki pełzania również ustawione są na zero ponieważ rozpatrujemy etap zaraz po przyłożeniu siły sprężającej. Jak widać wartość \(E_{ cm }\) – zostało ustawione na te samą wartość co w aplikacji Beam.
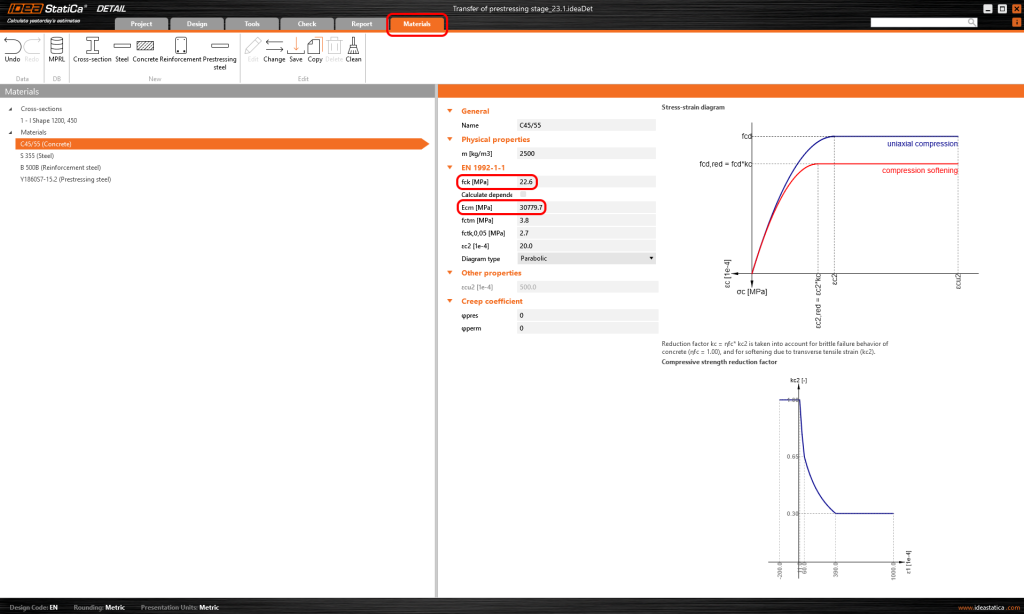
Porównajmy więc wyniki. Ponieważ nie wprowadziliśmy żadnego współczynnika pełzania oraz żadnych strat długoterminowych, nie ma różnicy między wynikami krótko i długoterminowymi.
Naprężenie w cięgnach dla SGU

Naprężenie w betonie dla SGU

Sprawdzenie SGU w Beam
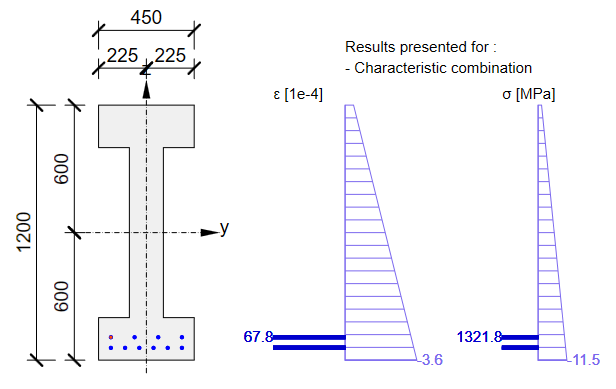

Jak widać wyniki są bardzo zbliżone. Wygląda więc na to że poprawnie udało nam się odwzorować pierwszy etap w Detail. Należy zwrócić uwagę na współczynniki \(r_{ inf }\) oraz \(r_{ sup }\) zdefiniowane w EN 1992-1-1; 5.10.9 (1) które w Beam ustawione są na wartość 1.0.
Z drugiej strony możemy oczekiwać znacznej różnicy w wynikach dla kombinacji SGN. Spowodowana jest ona stratami od odkształcenia sprężystego betonu \(\Delta\sigma_{ pe }\) która w Beam obliczana jest przy użyciu analizy liniowej a w Detail używając autorskiej metody CSFM.
- W podejściu liniowym (czyli w Beam), straty związane ze sprężystym odkształceniem betonu \(\Delta\sigma_{ pe }\) są takie same dla SGN i SGU. Powodem tego jest zastosowana analiza liniowa w której używany jest również liniowy model materiałowy z modułem sprężystości \(E_{ cm }\) obliczanym na podstawie \(f_{ ck }\) dla całości analizy (także dla analitycznego wyliczenia strat) i tylko dla sprawdzenia przekrojowego w kombinacji SGN używamy modułu sprężystości obliczonego z \(f_{ cd }\).
- Natomiast w aplikacji Detail, całość obliczeń dla SGN jest przeprowadzana na module sprężystości obliczonym z \(f_{ cd }\) (na który ma wpływ również współczynnik \(\eta_{ fc }\) ). Powoduje to większe odkształcenie sprężyste i w konsekwencji większe straty \(\Delta\sigma_{ pe }\). Warto przypomnieć że wprowadziliśmy naprężenie przed stratami spowodowanymi odkształceniem sprężystym. Te straty są obliczane na podstawie odkształcenia modelu z przyłożoną siłą sprężającą (w przypadku SGN z niższym modułem sprężystości).
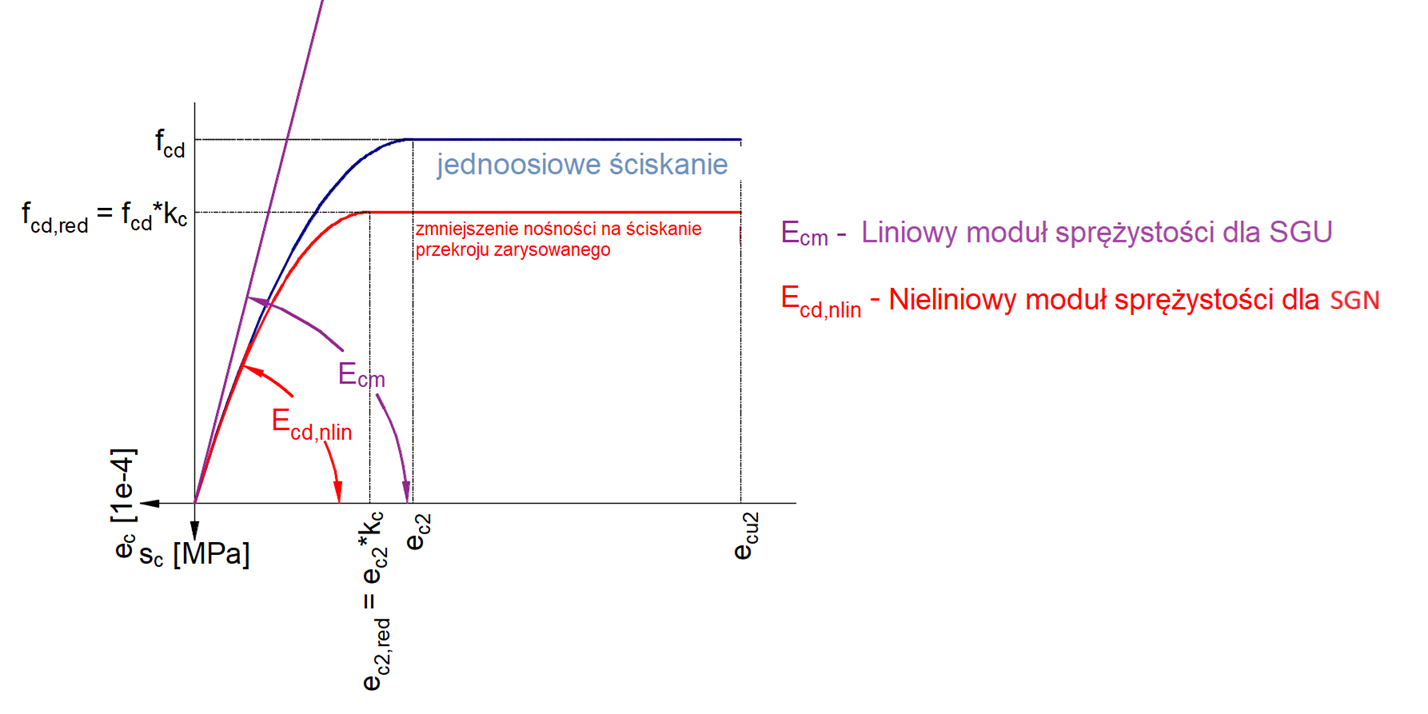
Zauważmy że SGU jest obliczane w Detail na podstawie \(E_{ cm }\) (niezależnego od \(f_{ ck }\)). Natomiast SGN jest obliczane na podstawie \(f_{ cd }\) z którego obliczany jest paraboliczny wykres naprężenie-odkształcenie.
Teraz wiemy już jak użyć aplikacji Detail do projektowania konstrukcji sprężonych na etapie zaraz po odcięciu cięgien. Możemy teraz dodać do modelu strefy nieciągłości np. otwory by zobaczyć pełne możliwości obliczeniowe programu.
Przyłożenie obciążeń
Na tym etapie wiek betonu wynosi 60 dni. Celem kalkulacji na tym etapie jest sprawdzenie zachowania naszej belki na początku jej projektowanego czasu życia z uwzględnieniem wszystkich obciążeń – w tym zmiennych. Dodane zostały obciążenie pozostałych dwóch natur. Obciążenia są oczywiście takie same jak w Beam.
Musimy określić dwie wartości konieczne do wpisania do Detail.
- Współczynnik pełzania dla czasu od 2 do 60 dni.
- Oszacowanie strat długoterminowych występujących między dniem 2 a 60.
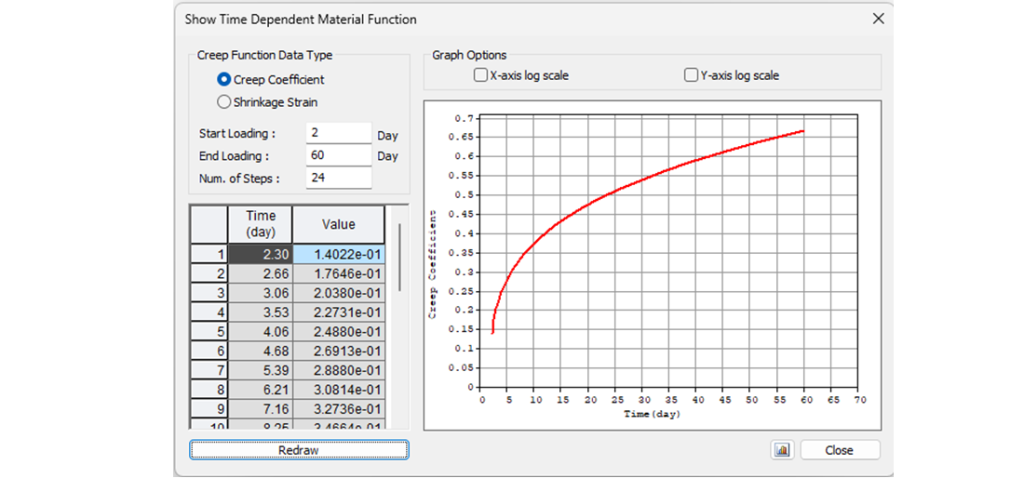
Zacznijmy od współczynnika pełzania. Na poniższym wykresie, widzimy funkcję pełzania od dnia2 do 60 dla betonu klasy C45/55 i cementu klasy R zgodnie z eurokodem. Wartość współczynnika pełzania jest więc równa \(\phi_{ pres }\approx\phi_{ (60) }-\phi_{ (2) } = 0,65-0,15 = 0,50\)
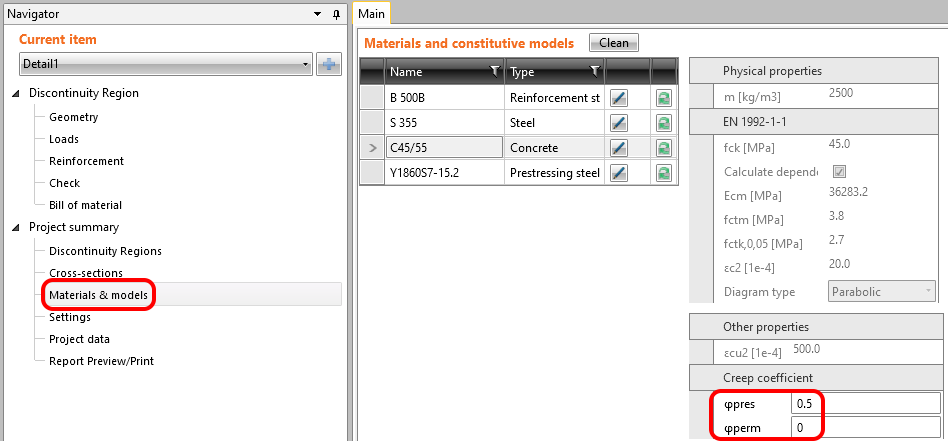
W Detail współczynnik pełzania może zostać ustawiony w zakładce Materiały i Modele. Oczywiste jest że wartość modułu sprężystości \(E_{ cm }\) musi zostać ustawiona na wartość domyślną (warto sobie w tym miejscu przypomnieć wykres z przedstawionymi inkrementacjami). Możemy również zauważyć że wartość \(\phi_{ perm }=0,0\) ponieważ chcemy przyłożyć obciążenia stałe jako obciążenie krótkotrwałe tak samo jak obciążenia zmienne.
W tym momencie musimy pomyśleć o stratach długoterminowych. Oczywiście możemy je oszacować (przyjęlibyśmy np. 10%). Jest to najprostszy sposób jednak w naszym przykładzie chcemy zrobić to w sposób dokładny. Dlatego policzymy \(\sigma_{ 60 }\) – naprężenie po 60 dniach strat (niebieska linia) w aplikacji Beam poprzez ustawienie czasu na 60 dni.
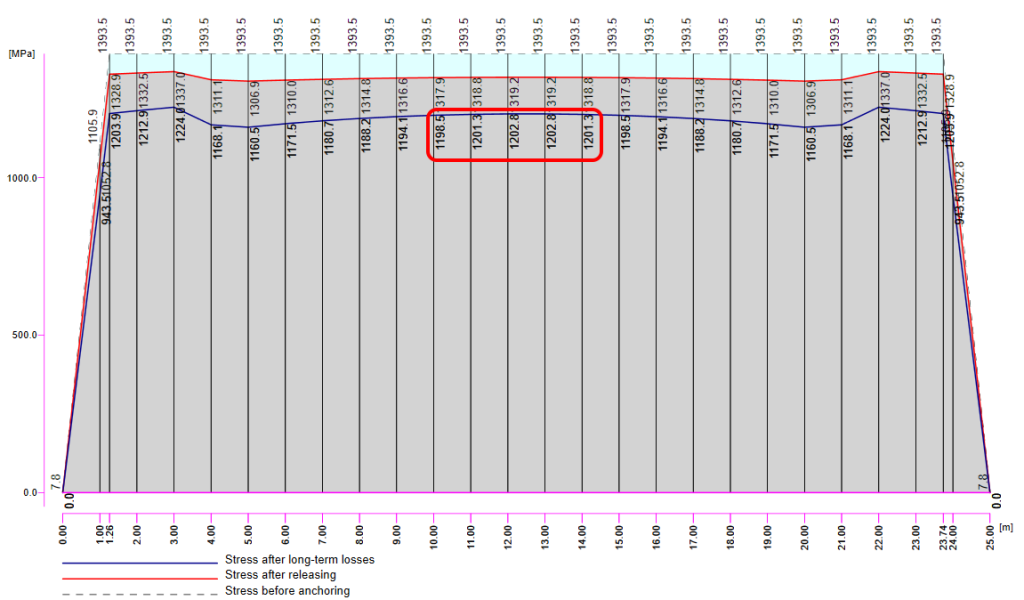
Wartość \(\sigma_{ 60 }=1200MPa\) widoczna jest na poniższym wykresie.
Następnie musimy policzyć model w aplikacji Detail z ustawionym współczynnikiem pełzania oraz zerowymi stratami długoterminowymi dla pierwszej inkrementacji – P100% by policzyć \(\sigma_{ det,60 }\). Ważną rzeczą jest to że musimy odczytać wyniki dla długoterminowych efektów by wziąć pod uwagę współczynnik pełzania.
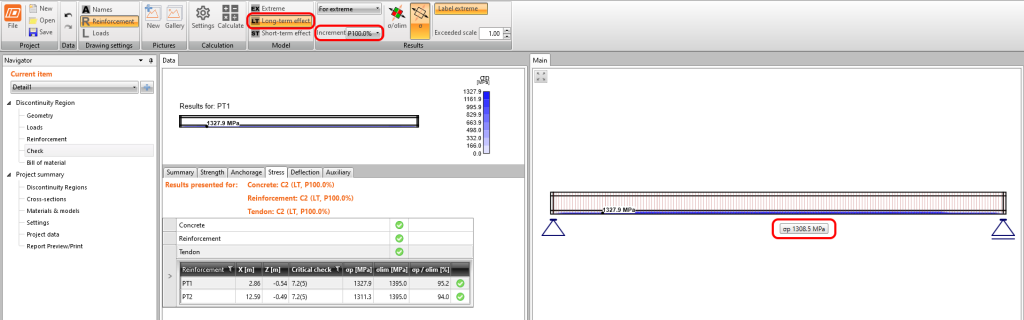
Na podstawie wyników otrzymujemy wartość \(\sigma_{ det,60 }=1308,5 MPa\).
Długoterminowe straty mogą być obliczone jako \(\sigma_{ 60 }/\sigma_{ det,60 }=1200/1308,5=0,91->\) wynoszą one 9%. Wprowadźmy te wartość i porównajmy nasze wyniki.
Wyniki są odczytywane dla strat długoterminowych (chcemy aby pełzanie i straty zostały uwzględnione) i dla wszystkich inkrementacji (chcemy aby wszystkie przypadki obciążenia były przyłożone).
Naprężenie w cięgnie dla SGU
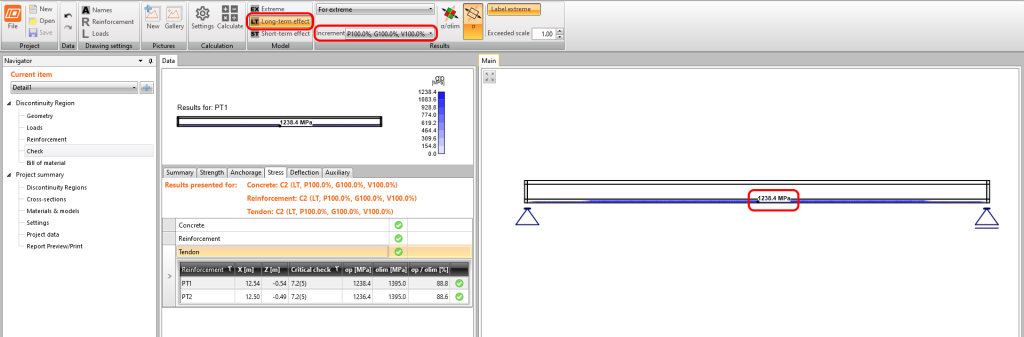
Naprężenie w betonie dla SGU

Wyniki SGU w Beam
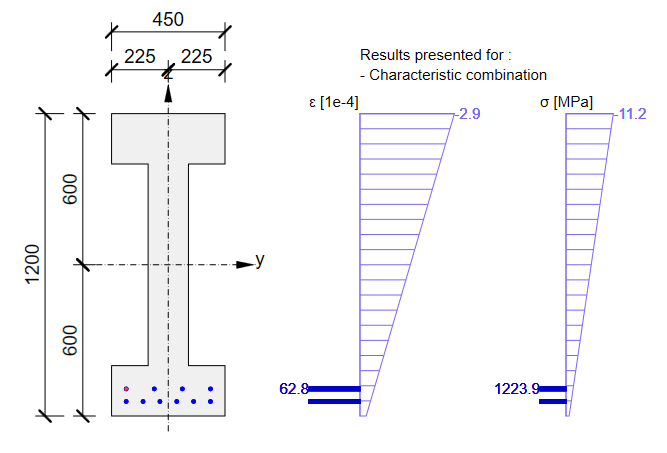

Ponownie otrzymujemy dużą zbieżność wyników. Wygląda na to że poprawnie zamodelowaliśmy ten etap. Dla SGN wystąpi ten sam problem co opisywany w poprzednim etapie. Zauważmy że współczynniki \(r_{ inf }\) oraz \(r_{ sup }\) zdefiniowane w EN 1992-1-1; 5.10.9 (1) nadal są ustawione na 1,0 w aplikacji Beam.
Teraz przypomnijmy sobie początek tego artykułu gdzie opisywaliśmy inkrementacje. W modelu w Detail dla tego etapu (do pobrania na dole) możemy przeanalizować poszczególne przypadki obciążeń. Możemy również sprawdzić efekty krótkoterminowe które będą się różniły od tych uzyskanych w modelu dla etapu poprzedniego. Powodem jest inny moduł sprężystości \(E_{ cm }\) używany do obliczeń.
W modelu możemy również zauważyć że dla efektów krótkoterminowych założono że etap pierwszego przeniesienia siły sprężającej został uwzględniony, ale po czasie t = 28 dni. Oznacza to że jeżeli nasze belki przeniosą siłę sprężającą dopiero po ponad 28 dniach (co w praktyce nie zdarza się zbyt często) to możemy zrezygnować z tworzenia dodatkowego modelu dla etapu pierwszego.
Koniec projektowanego czasu życia
Stosujemy to samo podejście co w poprzednim etapie. Na początku określamy współczynniki pełzania. Na poniższym wykresie widzimy przebieg funkcji wartości współczynnika pełzania w czasie.
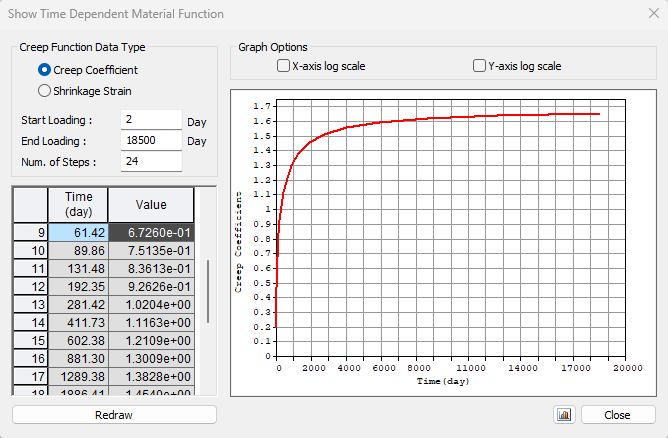
Wartość \(\phi_{ pres } \simeq 1,65\) dla czasu od drugiego do 18250 dnia dla cementu klasy R zgodnie z eurokodem. Wartość \(\phi_{ perm } = \phi_{ (18250) }-\phi_{ (60) } \simeq 1,65-0,65 =1,00\) dla czasu od 60 do 18250 dnia. Zauważmy podświetloną wartość \(\phi_{ (60) }\) w tabeli wyżej.
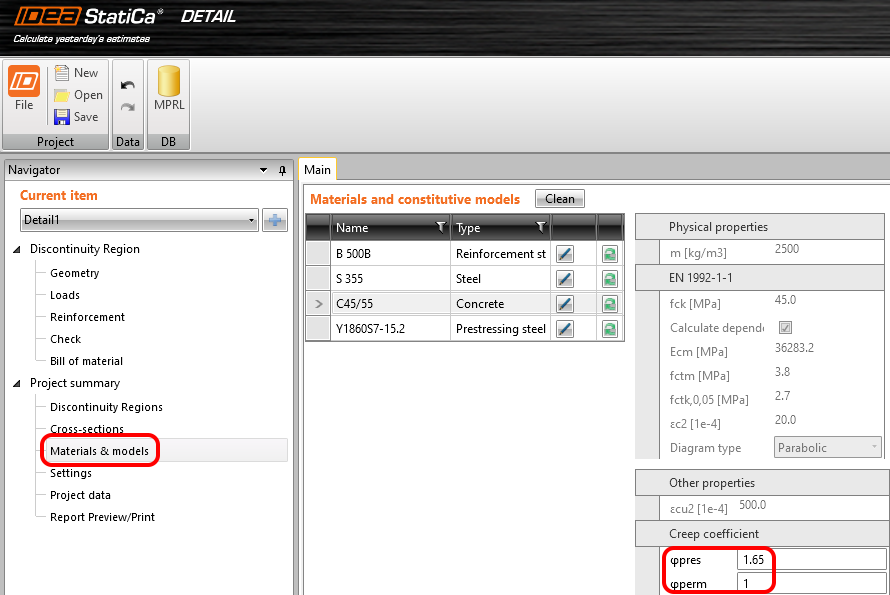
Potrzebujemy także strat długoterminowych. Dlatego ponownie używamy podejścia ze zdefiniowaniem współczynników pełzania i stratami długoterminowymi ustawionymi na 0 dla pierwszej inkrementacji P100%. Ważne jest również aby przy odczytywaniu wyników dla strat długoterminowych robić to z uwzględnionym współczynnikiem pełzania.
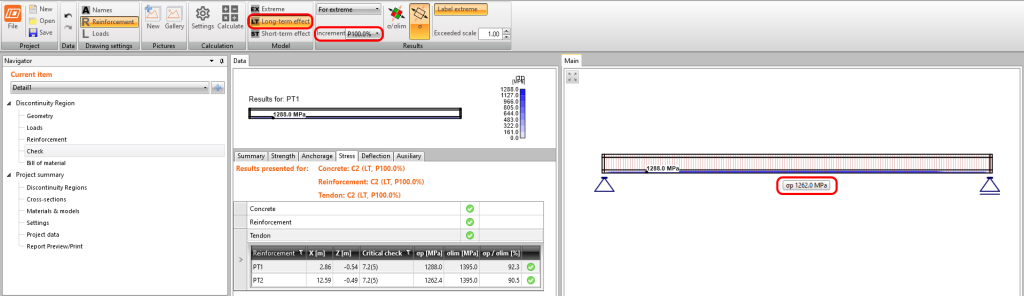
Straty długoterminowe mogą być obliczone jako \(\sigma_{ \infty }/\sigma_{ det, \infty }=1100/1267 = 0,868 ->\) straty długoterminowe wynoszą 13,2%. Wartość \(\sigma_{ \infty }\) jest obliczana pod wykresem naprężeń i strat w cięgnach. Wprowadźmy wartości i odczytajmy wyniki.
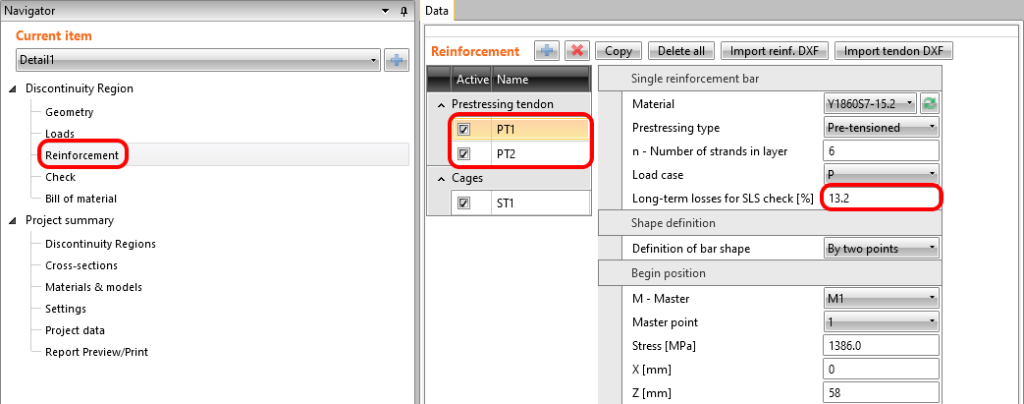
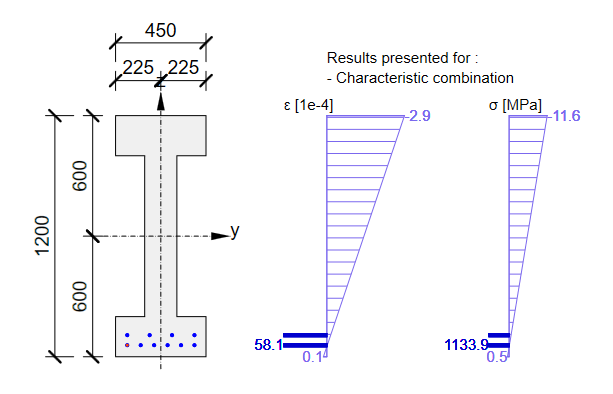
Naprężenia w cięgnach dla SGU
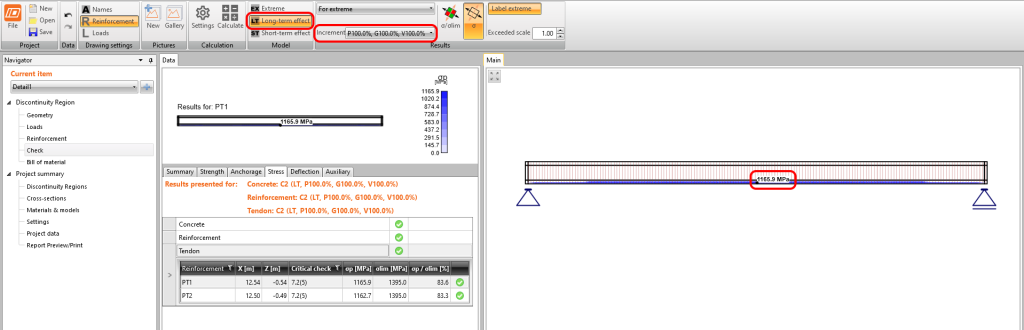
Naprężenia w betonie dla SGU
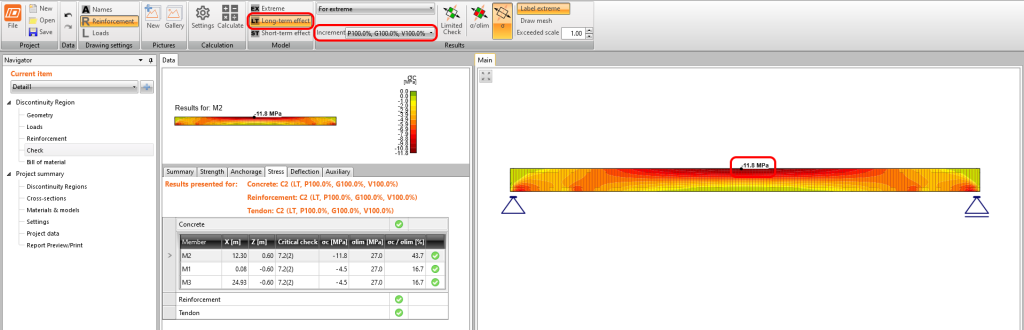
Sprawdzenie przekrojowe SGU z aplikacji Beam

Podsumowanie
Nareszcie udało nam się przejść przez wszystkie etapy. Stworzyliśmy procedurę projektowania elementów strunobetonowych w Detail a poniżej przedstawiamy jej algorytm.
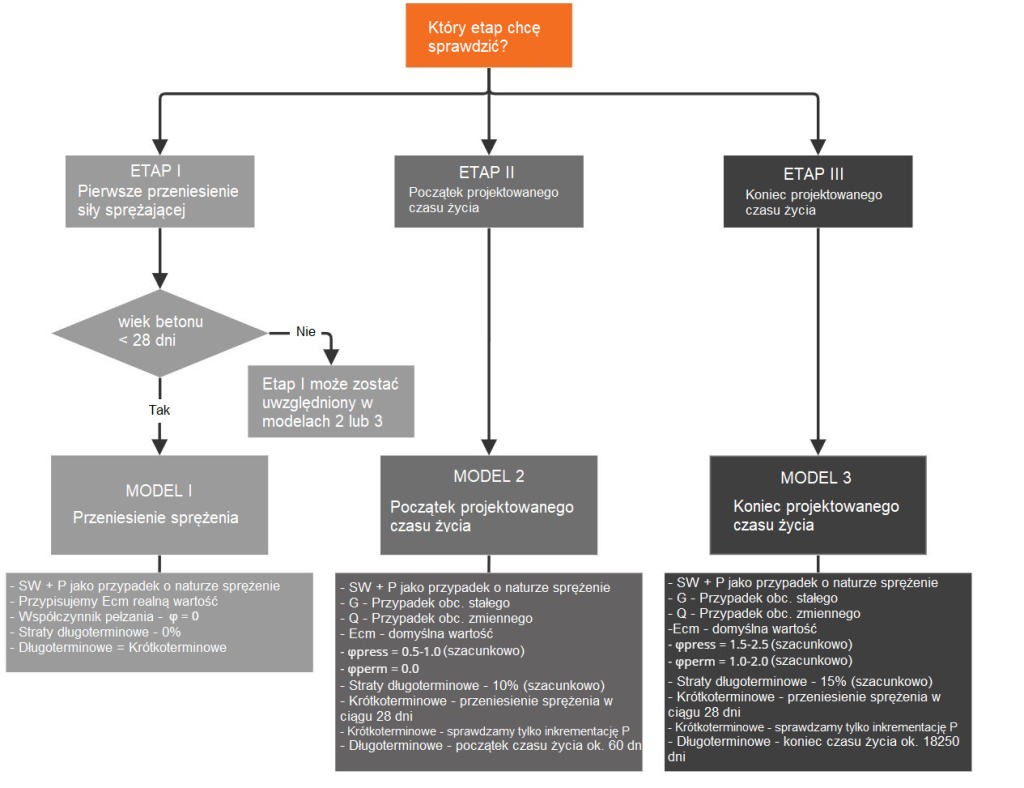
Warto w tym miejscu jeszcze raz powtórzyć że dla strunobetonu powinniśmy wprowadzić naprężenia zaraz po odcięciu strun (ale przed stratami od sprężystego odkształcenia betonu). Oszacowane straty długoterminowe od skurczu i relaksacji również muszą zostać wprowadzone. Straty pełzania są obliczane automatycznie.
Z powyższego wynika że dla modelów 1 i 3 dla efektów krótkotrwałych należy uwzględnić tylko pierwszą inkrementację P (ponieważ podczas sprężenia nie będą stosowane żadne inne obciążenia stałe lub zmienne). Podejście to obwiązuje tylko gdy wiek betonu w momencie pierwszego przeniesienia sprężenia jest większy niż 28 dni. W przeciwnym wypadku musimy stworzyć Model 1 – aby uwzględnić efekty krótkotrwałe.
Długoterminowe straty dla kombinacji SGN muszą zostać uwzględniony we współczynnikach kombinacji. Oszacowane straty które wprowadzamy w cięgnach w zakładce zbrojenie są brane pod uwagę dla SGU. Wprowadzenie oszacowanych na 15% strat powinno wyglądać w następujący sposób.
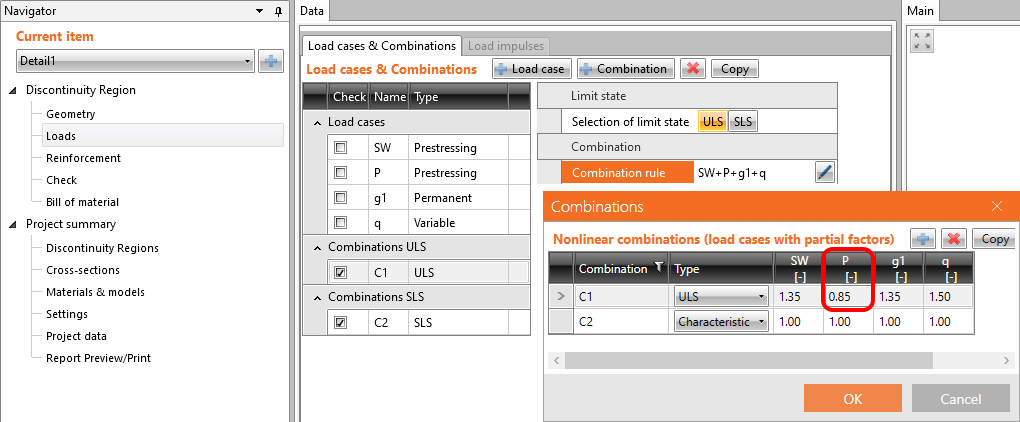
Współczynniki \(r_{ inf }\) oraz \(r_{ sup }\) zdefiniowane w EN 1992-1-1;5.10.9 (1) dla efektów sprężenia dla SGU powinny być także brane pod uwagę w kombinacjach. Oznacza to że powinniśmy stworzyć co najmniej dwie kombinacje.
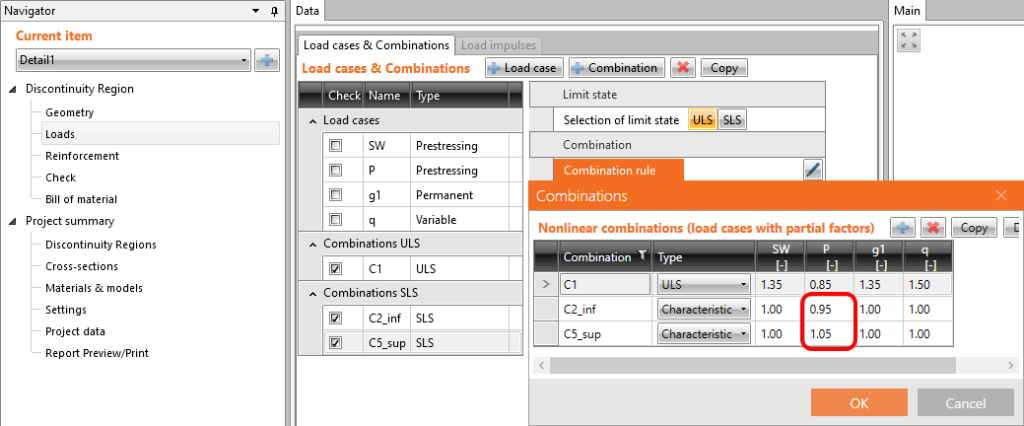
W powyższym artykule dowiedzieliśmy się jak używać IDEA StatiCa Detail do projektowania elementów strunobetonowych. Warto jednak pamiętać że główną rolą Detail jest wsparcie projektanta w obliczaniu stref nieciągłości np. belek z otworami. Dlatego mimo że jest on świetnym narzędziem również do projektowania prostych dźwigarów strunobetonowych nie należy zapominać o aplikacji Beam której tutaj użyliśmy do porównania wyników. W IDEA StatiCa Beam wprost zaimplementowane zostało etapowanie, oraz inne narzędzia znacznie usprawniające proces projektowy.
Pliki do pobrania:

